Class IX, NCERT (CBSE) Mathematics | Quadrilaterals, Introduction (Chapter 8.1)

Class IX, Mathematics (Quadrilaterals)

NCERT (CBSE) Textbook Exercise 8.1 Solution

(Page 146 - 147)

Question 1: The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral.

Ans:

Let us assume that the common ratio between the angles of quadrilateral be x. Therefore, the angles will be 3x, 5x, 9x, and 13x respectively.

As the sum of all interior angles of a quadrilateral is 360º, we can write

3x + 5x + 9x + 13x = 360º

or, 30x = 360º

or, x = 12º

Hence, the angles of the quadrilateral are

3x = 3 × 12 = 36º

5x = 5 × 12 = 60º

9x = 9 × 12 = 108º

13x = 13 × 12 = 156º

Question 2: If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Ans:

Let ABCD be a parallelogram. in order to show that ABCD is a rectangle, we have to prove that one of its interior angles of the ABCD is 90º.

Considering ΔABC and ΔDCB,

AB = DC (Opposite sides of a parallelogram are equal)

BC = BC (Common) and AC = DB (Given)

∴ ΔABC ≅ ΔDCB (By SSS Congruence rule)

∠ABC = ∠DCB (as the sum of the measures of angles on the same side of transversal is 180º).

or, ∠ABC + ∠DCB = 180º (AB || CD)

or, ∠ABC + ∠ABC = 180º

or, 2∠ABC = 180º

or, ∠ABC = 90º

Since ABCD is a parallelogram and one of its interior angles is 90º so ABCD is a rectangle.

Question 3: Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Ans: 

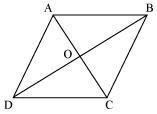Let us consider ABCD a quadrilateral, whose diagonals AC and BD bisect each other at right angle i.e., OA = OC, OB = OD, and 
∠AOB = ∠BOC = ∠COD = ∠AOD = 90º. 
For ABCD to be a rhombus, we have to prove that ABCD is a parallelogram and all the sides of ABCD are equal.

Now considering ΔAOD and ΔCOD,

OA = OC (Diagonals bisect each other) 

∠AOD = ∠COD (Given)

OD = OD (Common)

ΔAOD ≅ ΔCOD (By SAS congruence rule)

∴ AD = CD . . . . . . (1)

In the same way, it can be proved that

AD = AB and CD = BC . . . . . . (2)

From equations (1) and (2), we get

AB = BC = CD = AD

Since opposite sides of quadrilateral ABCD are equal, so ABCD is a parallelogram. Also since all sides of parallelogram ABCD are equal, so ABCD is a rhombus.

Question 4: Show that the diagonals of a square are equal and bisect each other at right angles.

Ans:

Let us consider a square ABCD whose diagonals AC and BD intersect each other at a point O. To prove that the diagonals of a square are equal and bisect each other at right angles, we have to prove AC = BD, OA = OC, OB = OD, and ∠AOB = 90º.

Considering ΔABC and ΔDCB,

AB = DC (Sides of a square are equal)

∠ABC = ∠DCB (All interior angles are of 90 ) BC = CB (Common side)

∴ ΔABC ≅ ΔDCB (By SAS congruency)

∴ AC = DB (By CPCT)

Hence, the diagonals of the square ABCD are equal in length.

Now considering ΔAOB and ΔCOD,

∠AOB = ∠COD (Vertically opposite angles)

∠ABO = ∠CDO (Alternate interior angles)

AB = CD (Sides of a square are equal)

∴ ΔAOB ≅ ΔCOD (By AAS congruence rule)

∴ AO = CO and OB = OD (By CPCT)

Hence, the diagonals of ABCD (square) bisect each other.

Similarly in ΔAOB and ΔCOB,

As we had proved that diagonals bisect each other, therefore,

AO = CO; AB = CB (Sides of a square are equal); BO = BO (Common)

∴ ΔAOB ≅ ΔCOB (By SSS congruency)

∴ ∠AOB = ∠COB (By CPCT)

∠AOB + ∠COB = 180º (Linear pair)

or, 2∠AOB = 180º

or, ∠AOB = 90º

Hence proved that the diagonals of a square bisect each other at right angles.

Question 5: Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Ans:

Consider a quadrilateral ABCD whose diagonals AC and BD intersect each other at O. It is given that the diagonals of ABCD are equal and bisect each other at right angles. Therefore, AC = BD, OA = OC, OB = OD, and ∠AOB = ∠BOC = ∠COD = ∠AOD = 90º. To prove ABCD is a square, we have to show that ABCD is a parallelogram where AB = BC = CD = AD, and one of its interior angles is 90º.

Consider ΔAOB and ΔCOD,  
AO = CO (Diagonals bisect each other)

OB = OD (Diagonals bisect each other)

∠AOB = ∠COD (Vertically opposite angles)

∴ ΔAOB ≅ ΔCOD (SAS congruence rule)

∴ AB = CD (By CPCT)  . . . . . . . . . . . . (1)

Also, ∠OAB = ∠OCD (By CPCT)

However, these angles are alternate interior angles of  AB and CD and alternate interior angles are equal to each other only when the two lines are parallel.

∴ AB || CD  . . . . . . . . . . . . . . . (2)

From equations (1) and (2), we can say that

ABCD is a parallelogram.

Consider ΔAOD and ΔCOD,

AO = CO (Diagonals bisect each other)

∠AOD = ∠COD (Given that each is 90º)

OD = OD (Common)

∴ ΔAOD ≅ ΔCOD (SAS congruence rule)

∴ AD = DC  . . . . . . . . . . . . . (3)

But, AD = BC and AB = CD (Opposite sides of parallelogram ABCD)

∴ AB = BC = CD = DA

Therefore, all the sides of quadrilateral ABCD are equal to each other.

Consider ΔADC and ΔBCD,

AD = BC (Already proved)

AC = BD (Given)

DC = CD (Common)

∴ ΔADC ≅ ΔBCD (SSS Congruence rule)

∴ ∠ADC = ∠BCD (By CPCT)

However, ∠ADC + ∠BCD = 180° (Co-interior angles)

or, ∠ADC + ∠ADC = 180°

or, 2∠ADC = 180°

or, ∠ADC = 90°

One of the interior angles of quadrilateral ABCD is a right angle.

Therefore ABCD is a parallelogram, AB = BC = CD = AD and one of its interior angles is 90º. Hence, ABCD is a square.

Question 6: Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that

(i) It bisects ∠C also,

(ii) ABCD is a rhombus.

Ans:

 (i) ABCD is a parallelogram.

∴ ∠DAC = ∠BCA (Alternate interior angles)  . . . . . . (1)

And, ∠BAC = ∠DCA (Alternate interior angles)  . . . . . . . . (2)

Given that AC bisects ∠A.

so, ∠DAC = ∠BAC  . . . . . . . . (3)

From the above equations (1), (2), and (3), we get

∠DAC = ∠BCA = ∠BAC = ∠DCA  . . . . . . . . . . (4)

or,  ∠DCA = ∠BCA

Hence, AC bisects ∠C.

(ii) 
From equation (4), we obtain

∠DAC = ∠DCA

or, DA = DC (Side opposite to equal angles are equal)

DA = BC and AB = CD (Opposite sides of a parallelogram)

∴ AB = BC = CD = DA

Hence, ABCD is a rhombus.

Question 7: ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

Ans:

Let us join AC.

In ΔABC,

BC = AB (as sides of a rhombus are equal to each other)

∠1 = ∠2 (Angles opposite to equal sides of a triangle are equal)

However, ∠1 = ∠3 (Alternate interior angles for parallel lines AB and CD)

or, ∠2 = ∠3

Therefore, AC bisects ∠C.

∠2 = ∠4 (Alternate interior angles for || lines BC and DA)

or, ∠1 = ∠4

Therefore, AC bisects ∠A.

In the same way it can be proved that BD bisects ∠B and ∠D as well.

Question 8:

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:

(i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

Ans: 

 









(i) As per the given conditions ABCD is a rectangle. whose ∠A = ∠C

CD = DA (Sides opposite to equal angles are also equal)

However, DA = BC and AB = CD (Opposite sides of a rectangle are equal)

∴ AB = BC = CD = DA

Therefore, ABCD is a rectangle whose all sides are equal.

Hence, ABCD is a square.

(ii) Let us join BD and in ΔBCD,

BC = CD (Sides of a square are equal to each other)

∠CDB = ∠CBD (Angles opposite to equal sides are equal)

However, ∠CDB = ∠ABD (Alternate interior angles for AB || CD)

∠CBD = ∠ABD 
or, BD bisects B.

Also, ∠CBD = ∠ADB (Alternate interior angles for BC || AD)

∠CDB = ∠ABD 
Hence, BD bisects ∠D.

Question 9: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:

(i) ΔAPD ≅ ΔCQB

(ii) AP = CQ

(iii) ΔAQB ≅ ΔCPD

(iv) AQ = CP

(v) APCQ is a parallelogram

Ans:

(i) Consider ΔAPD and ΔCQB,

∠ADP = ∠CBQ (Alternate interior angles for BC || AD)

AD = CB (Opposite sides of parallelogram ABCD)

DP = BQ (Given)

∴ ΔAPD ≅ ΔCQB (Using SAS congruence rule)

(ii) As we had observed that ΔAPD ≅ ΔCQB,

∴ AP = CQ (CPCT)

(iii) Consider ΔAQB and ΔCPD,

∠ABQ = ∠CDP (Alternate interior angles for AB || CD)

AB = CD (Opposite sides of parallelogram ABCD)

BQ = DP (Given) 
Therefore, ΔAQB ≅ ΔCPD (Using SAS congruence rule)

(iv) As we had observed that ΔAQB ≅ ΔCPD,

∴ AQ = CP (CPCT)

(v) From the results obtained in (ii) and (iv) above,

AQ = CP and

AP = CQ

Since opposite sides in quadrilateral APCQ are equal to each other so, APCQ is a parallelogram.

Question 10: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that 

(i) ΔAPB ≅ ΔCQD

(ii) AP = CQ

Ans:

(i) In ΔAPB and ΔCQD,

∠APB = ∠CQD (Each 90°)

AB = CD (Opposite sides of parallelogram ABCD)

∠ABP = ∠CDQ (Alternate interior angles for AB || CD)

∴ ΔAPB ≅ ΔCQD (By AAS congruency)

(ii) By using the above result

ΔAPB ≅ ΔCQD, we obtain

AP = CQ (By CPCT)

Question 11: In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that

(i) Quadrilateral ABED is a parallelogram

(ii) Quadrilateral BEFC is a parallelogram

(iii) AD || CF and AD = CF

(iv) Quadrilateral ACFD is a parallelogram

(v) AC = DF

(vi) ΔABC ≅ ΔDEF.

Ans:

(i) Given that AB = DE and AB || DE.

If two opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.

Therefore, quadrilateral ABED is a parallelogram.

(ii) Also, BC = EF and BC || EF

Therefore, quadrilateral BCEF is a parallelogram.

(iii) As ABED and BEFC are parallelograms, therefore

AD = BE and AD || BE

(Opposite sides of a parallelogram are equal and parallel)

And, BE = CF and BE || CF

(Opposite sides of a parallelogram are equal and parallel)

∴ AD = CF and AD || CF

(iv) We had already observed that one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and parallel to each other, therefore, it is a parallelogram.

(v) As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other. 
i.e. AC || DF and AC = DF

(vi) Consider ΔABC and ΔDEF,

AB = DE (Given)

BC = EF (Given)

AC = DF (ACFD is a parallelogram)

∴ ΔABC ≅ ΔDEF (By SSS congruence rule)

Question 12: ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that

(i) ∠A = ∠B (ii) ∠C = ∠D

(iii) ΔABC ≅ ΔBAD (iv) diagonal AC = diagonal BD

Ans:

First extend AB. Now draw a line through C, which is parallel to AD, intersecting AE at point E. It is clear that AECD is a parallelogram.

(i) AD = CE (Opposite sides of parallelogram AECD)

However, AD = BC (Given)

Therefore, BC = CE

∠CEB = ∠CBE (Angle opposite to equal sides are also equal)

Considering the parallel lines AD and CE then AE which is a  transversal line for them.
We have,

∠A + ∠CEB = 180º (Angles on the same side of transversal)

∠A + ∠CBE = 180º (Using the relation∠CEB = ∠CBE)  . . . . . . . (1)

However, ∠B + ∠CBE = 180º (Linear pair angles)  . . . . . . . . (2)

From the equations (1) and (2), we obtain

∠A = ∠B

(ii) AB || CD

∠A + ∠D = 180º (Angles on the same side of the transversal)

Also, ∠C + ∠B = 180° (Angles on the same side of the transversal) 
so, ∠A + ∠D = ∠C + ∠B

However, ∠A = ∠B [Using the result obtained in (i)]
or, ∠C = ∠D

(iii) Consider ΔABC and ΔBAD,

AB = BA (Common side) BC = AD (Given)

∠B = ∠A (already proved )

∴ ΔABC ≅ ΔBAD (by SAS congruence rule)

(iv) ΔABC ≅ ΔBAD 
Therefore, AC = BD (By CPCT)